Jay's Slide RulesI'm not sure why it took me so long to get it? As a math teacher, you'd think that math-related gizmos would resonate with my inner being, but it wasn't until recently that I stumbled across a collection of slide rules at an estate sale...and I knew that I had to have them.
To say this started the dive down a deep rabbit hole is an understatement. Once I learned how to use them, coupled with their virtues educationally that I feel are missing in the calculator-age, further combined with the ease of finding them...my collection started growing exponentially...pun intended. What follows is documentation; a written and picture record of my collection. But more than that, it'll be a place where I can explore the slide rule universe and contribute something back to it. Articles on the site, much like my Astronomy articles, are more like books than they are blog posts or essays. Read them a little, digest some of it, and then come back for more. Each of the major slide rule manufacturers will likely have their own dedicated webpage, full of historical information and samples of slide rules from my own collection. These individual pages have the potential to turn into something far more ambitious, as has happened to my page about Keuffel & Esser (K&E). As such, these pages will always be under construction, as they represent a living, changing documentation of my own learning. At any time, you could consider such pages "complete," but you should know that they often go through many revisions over time. 
This image of the K&E Celanese Celcon slide rule might not be as awesome as one of my galaxy images on my main page, but you can't convince me of that! They get the same photographic treatment in my mind.
What Good are Slide Rules Anyway?Just because nobody uses slide rules anymore, it doesn't mean they are without value. In fact, anybody today who knows how to use one will be quick to tell you how much value they retain as an educational tool. No, what you are reading right now wasn't written in the 1980s. I am proclaiming that in the decade of the 2020s, math education would be significantly enhanced and improved for students at ALL ages if they gain at least some experience with a slide rule. Analog in a digital age? Yes...you might be surprised what it can teach!
I've written an entire article about what I'm talking about here, called "The Educational Value of Slide Rules." Click on the link to open a new window, where you will learn ten specific ways that slide rules can enhance student learning and performance in mathematics. And for teachers, the article is FILLED with activities to use with your own students. You'll probably even be able to use a slide rule after reading it! |
My Favorite Slide RulesMy favorite thing about slide rules is how they feel in your hands. It's much like a telescope or a guitar in that regard...if you like the way it feels - the heft, the action, the smoothness - then you are more likely to want to use a slide rule. And these become the ones you like the most. As a collector, perhaps your favorites will be those that were harder to come by. Maybe its the rare rule in your collection that is also your most valuable. But for me, it's the one I enjoy holding the most.
Well, that's partially true. This slide rule barely fits in your hand... 
Found on Craigslist in Austin and picked up by my cousin, Brady, this is my K&E Deci-Lon demonstration slide rule. Once property of Mineola ISD here in Texas, as shown on the still affixed inventory tag, this 6.5 foot slide rule used to hang in a high school classroom. Many such rules exist, including two Picketts, the N1010-ES and N902-ES demonstration rules that I also own. But this one is just cool...and quite rare. It now hangs in my OWN math classroom. Many of my slide rules have similar stories which endear them to me beyond how they feel in my hand. These too become favorites. I'll be adding all of my collection to this site at some point, but for now, if you want to know what my favorites are, then let's just jump right into them from here...MY FAVORITE SLIDE RULES. 
My slide rule collection on full display in my classroom.
|
New to the Collection...
Slide Rule Basics
With two rulers, who needs a fancy calculator to add numbers? Clearly, from the image shown at right...
3 + 1 = 4
3 + 2 = 5
3 + 3 = 6
3 + 4 = 7
3 + 5 = 8
This works if all the major divisions are counted by ones (in inches or centimeters, doesn't matter). If you wanted to add bigger numbers, you could either extend the scale OR you could mentally add 10 to the existing numbers. For example, instead, the above rulers could read 13 + 4 = 17 or 13 + 14 = 27 just as easily as 3 + 4 = 7. And if you want to add numbers to something other than a 3, you just SLIDE the rulers. As such, this would be a slide rule for addition.
3 + 1 = 4
3 + 2 = 5
3 + 3 = 6
3 + 4 = 7
3 + 5 = 8
This works if all the major divisions are counted by ones (in inches or centimeters, doesn't matter). If you wanted to add bigger numbers, you could either extend the scale OR you could mentally add 10 to the existing numbers. For example, instead, the above rulers could read 13 + 4 = 17 or 13 + 14 = 27 just as easily as 3 + 4 = 7. And if you want to add numbers to something other than a 3, you just SLIDE the rulers. As such, this would be a slide rule for addition.
Now, how might you multiply numbers? Once again, let's look at these rulers...
|
Instead of a linear scale, what if each major "tick" is double the previous one? In this case, powers of two. Now, using the same technique as the "addition" slide rule, notice that the rulers are set up to do multiples of 4...
4 x 1 = 4 4 x 2 = 8 4 x 4 = 16 4 x 8 = 32 4 x 16 = 64 |
|
Thinking in this way, where a major division on the rule is always double the previous mark, you could then fill in the gaps between the divisions in order to multiply numbers other than multiples of two. For example, if half-way between 2 and 4 on the pink rule represents 3, then notice, shown at right, how 4 x 3 would line up with the midpoint between 8 and 16 on the upper rule. This number, 12, of course being the product of 4 x 3. From this we can also see that...
4 x 6 = 24 and 4 x 12 = 48
At that point, the numbers 5, 7, and 9 are the only missing whole numbers we need to place on our rulers (as midpoints) in order to do any multiplication we'd like. And if we construct these rulers in a way that let's them slide against each other, then we can make our own slide rules quite easily.
This idea of laying out the rulers in such a way, as logarithmic scales, is the fundamental basis for every slide rule we know. For more depth on "logarithmic scales" and the math behind them, please see this link here.
Now these images of rulers with stick-on numbers provides nothing in the way of accuracy, but you can begin to see that if we properly manufactured the scales with very fine, often etched marks...and if instead of going to 64 on the scales and only went to the number 10, with divisions spread across the entire ruler, then we can greatly lift the precision of the computations to as many as 3 significant figures on most slide rules.
4 x 6 = 24 and 4 x 12 = 48
At that point, the numbers 5, 7, and 9 are the only missing whole numbers we need to place on our rulers (as midpoints) in order to do any multiplication we'd like. And if we construct these rulers in a way that let's them slide against each other, then we can make our own slide rules quite easily.
This idea of laying out the rulers in such a way, as logarithmic scales, is the fundamental basis for every slide rule we know. For more depth on "logarithmic scales" and the math behind them, please see this link here.
Now these images of rulers with stick-on numbers provides nothing in the way of accuracy, but you can begin to see that if we properly manufactured the scales with very fine, often etched marks...and if instead of going to 64 on the scales and only went to the number 10, with divisions spread across the entire ruler, then we can greatly lift the precision of the computations to as many as 3 significant figures on most slide rules.
|
Most slide rules have "C" and "D" scales, and in the case of this nice K&E Jet-log "pocket" slide rule, shown at right, the scales show all logs between 1 and 10.
By showing this single "decade" of base 10 powers, the rule has enough resolution to do multiplication of numbers up to three significant figures. |
Looking at the C and D scales, notice that all of the marks in between the "powers of 2" obscures the fact that the distance between 2 and 4 and 8 are consistent on the rule. This makes them "logarithmic" scales. Such a scale is easy to lay out. Note that 3.16 is roughly the middle of the rule. This is because the log 3.16 is approximately 0.5, or 50% across the scale. If the 2 looks like it's 30% across the scale, it's because log 2 evaluates approximately to .301. The 9 on the scale is close to the 10 (written as 1) because log 9 = .954, or 95% of the distance across the scale.
|
|
At right, I have aligned the 1 on the C-scale (called the C scale "index") with the 3 on the D scale. You can get a variety of products, such as log 3 (on D) plus log 2 (on C) = log 6 (on D), which computes 2 * 3 = 6. Or, you may note that "1 over 3" and "2 over 6" and "3 over 9" shows proportions or equivalent fractions. How about under the hair-line of the cursor? This shows log 3 + log 2.2 = log 6.6 (or 3 x 2.2 = 6.6). But because this is a "decade" rule, note that you could compute this as 3 x 22 = 66 or 30 x 22 = 660 or even 300 x 220 is 66000.
This is the nature of slide rules...you are given the significant digits but you have to track your OWN decimal! |
The sum of two logs with the same base is equal to the the product of the arguments (inputs) of the logs. This log property is the heart of what makes multiplication (and division) possible with a slide rule. Here, we see the linear distance on the D scale of the log 3 + log 2.2 (under the cursor on the C scale) is equal to the log 6.6 (under the cursor on the D scale). The represents the product 3 * 2.2 = 6.6.
|
Division works in reverse, of course. Using the last image, to divide 6 by 2 (or in this case 60 by 20) you'd just read the answer under the 1 of the C-scale left "index." Note that 9 divided by 3 and 7.5 divided by 2.5 are also 3!
On almost any slide rule, you will find these C and D scales, which exist to perform the operations of multiplication and division. From there, you can create other scales that do a variety of functions. For example, I could square all the numbers on the D-scale and create my own "squared scale," which is typically the A and B scales on a slide rule. I could cube the values on the D-scale and produce a cubic scale, which is typically the K-scale on most slide rules. Using these squared or cubic scales in reverse would give you the ability to compute roots of numbers. L and LL scales typically allow for performing exponentials and logarithms of numbers. S and T scales will let you get the sine and tangent of angles listed on those scales (read off either the A-scale or D-scale, depending on the rule). Inverse (denoted with an "I" in a scale name) and folded scales ( denoted with an "F" in a scale name) allow you to perform inverse operations and multiple "chains" of operations in a row with less movement of the slide.
There are a variety of typical ways that all of these popular scales are laid out on a slide rule, slide rule "designs" which include Rietz, Mannheim, and Darmstadt rules, to list but a few. And because there might be a need to do advanced math, engineering, electronics, chemistry, business, and unit conversions using the same type "technology," then it opens up a world of variety when it comes to slide rule design. Basic rules with only the A, B, C, D, K, S, and T scales likely only require room on the front of a slide rule, leaving space on the back for a listing of formulas. This is known as a simplex design. But when you fill up a rule with more than 30 scales of a variety of powerful functions, then a slide rule might have scales on both front and back of the rule, which is referred to as a duplex design.
But fundamentally, if you begin by learning to use the scales of a slide rule to do basic arithmetic, then you can branch out into a universe of possibilities when it comes to slide rules, which is why they are so awesome to use and collect!
On almost any slide rule, you will find these C and D scales, which exist to perform the operations of multiplication and division. From there, you can create other scales that do a variety of functions. For example, I could square all the numbers on the D-scale and create my own "squared scale," which is typically the A and B scales on a slide rule. I could cube the values on the D-scale and produce a cubic scale, which is typically the K-scale on most slide rules. Using these squared or cubic scales in reverse would give you the ability to compute roots of numbers. L and LL scales typically allow for performing exponentials and logarithms of numbers. S and T scales will let you get the sine and tangent of angles listed on those scales (read off either the A-scale or D-scale, depending on the rule). Inverse (denoted with an "I" in a scale name) and folded scales ( denoted with an "F" in a scale name) allow you to perform inverse operations and multiple "chains" of operations in a row with less movement of the slide.
There are a variety of typical ways that all of these popular scales are laid out on a slide rule, slide rule "designs" which include Rietz, Mannheim, and Darmstadt rules, to list but a few. And because there might be a need to do advanced math, engineering, electronics, chemistry, business, and unit conversions using the same type "technology," then it opens up a world of variety when it comes to slide rule design. Basic rules with only the A, B, C, D, K, S, and T scales likely only require room on the front of a slide rule, leaving space on the back for a listing of formulas. This is known as a simplex design. But when you fill up a rule with more than 30 scales of a variety of powerful functions, then a slide rule might have scales on both front and back of the rule, which is referred to as a duplex design.
But fundamentally, if you begin by learning to use the scales of a slide rule to do basic arithmetic, then you can branch out into a universe of possibilities when it comes to slide rules, which is why they are so awesome to use and collect!
Types of Slide Rules
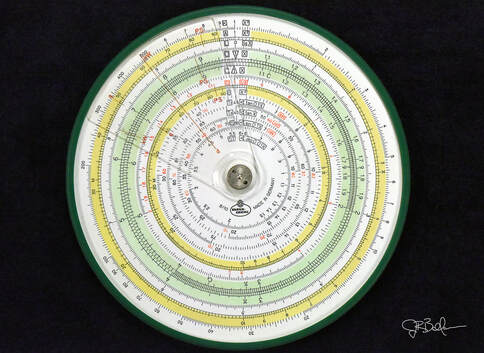
Given the wide range of functionality in a slide rule, there is an enormous range in which we could categorize them. However, they are typically organized in three ways...by maker, by function, and by design.
The portfolio - featured rules in my collection - below shows the major makers of slide rules by which my catalog will be organized. A full-page will be devoted to each maker, whereas the "Miscellaneous" category will be of slide rules of which I have very few OR a merely makers that I know too little about to devote the time and energy to a full page.
Within each maker page, eventually, there will be a history of the rules from that maker. They might be organized by their function, which is typically either for "general-purpose" math or "specialty" use. General-purpose rules are those that let you do math, and they range up in capability depending on their complexity and number of scales. The same could also be said about specialty rules; however, their focus is on a general task, such as electronics, chemistry, military, and any number of strange and delightful purposes. The specialty rules often allow the user to do most of the normal math computations, coupled with a scale or three added added utility in its intended discipline. Other specialty rules are almost entirely for the discipline for which they are designed, whereas a casual look provides nothing familiar to the ordinary person.
Finally, slide rules could be organized and described by design. The popular designs of slide rules are typically linear (like a ruler), circular (like a [ahem] circle), and cylindrical/spiral. The latter type of rules have prohibitive costs due to manufacturing costs and rarity - so there are naturally fewer such rules here - though I am not devoid of possessing a few!
In it's fully realized presentation, this website will feature each rule suitably photographed and a list of specifications. I will also include my own thoughts about the slide rule itself. All these things, of course, will be accomplished as time permits!
The portfolio - featured rules in my collection - below shows the major makers of slide rules by which my catalog will be organized. A full-page will be devoted to each maker, whereas the "Miscellaneous" category will be of slide rules of which I have very few OR a merely makers that I know too little about to devote the time and energy to a full page.
Within each maker page, eventually, there will be a history of the rules from that maker. They might be organized by their function, which is typically either for "general-purpose" math or "specialty" use. General-purpose rules are those that let you do math, and they range up in capability depending on their complexity and number of scales. The same could also be said about specialty rules; however, their focus is on a general task, such as electronics, chemistry, military, and any number of strange and delightful purposes. The specialty rules often allow the user to do most of the normal math computations, coupled with a scale or three added added utility in its intended discipline. Other specialty rules are almost entirely for the discipline for which they are designed, whereas a casual look provides nothing familiar to the ordinary person.
Finally, slide rules could be organized and described by design. The popular designs of slide rules are typically linear (like a ruler), circular (like a [ahem] circle), and cylindrical/spiral. The latter type of rules have prohibitive costs due to manufacturing costs and rarity - so there are naturally fewer such rules here - though I am not devoid of possessing a few!
In it's fully realized presentation, this website will feature each rule suitably photographed and a list of specifications. I will also include my own thoughts about the slide rule itself. All these things, of course, will be accomplished as time permits!
